2.1.6 Effective mass and eigenfrequency of the cantilever
In AFM, there exist techniques that are based not only on static beam deflection detection but also on cantilever vibration. To use them one should know the cantilever resonant frequency.
Let us calculate the resonant frequency of isotropic cantilever with mass
in the form of parallepiped having length
,
thickness
(
) and width
(
) to the free end of which the vertical point force
is applied (Fig. 1).
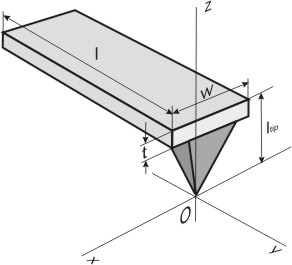
Fig. 1. Rectangular cantilever with a tip.
Determine kinetic
and potential
energy of the cantilever. Consider the beam element having length
at distance
from the fixed end. Kinetic energy of such an element is given by:
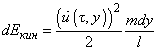
(1)
where
– displacements of the beam axial points at distance
from the fixed end at time
. Using formulas (8), (9) from chapter 2.1.2,
can be obtained as a function of the beam free end deflection
:
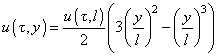
(2)
Substituting the expression for
into (1) and integrating over the beam length, we get:
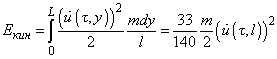
(3)
Potential energy calculation is easier. Because the point force
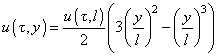acts only on the free end,
is evidently equal to the work done to move the beam end the distance
:
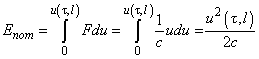
(4)
where
– coefficient of normal stiffness defined by formula (12) in chapter 2.1.2.
If system vibrations are considered to occur without total energy
dissipation, i.e.
, then, differentiating
with respect to time, we get equation of the cantilever free end move:
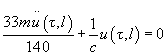
(5)
Therefore, the cantilever effective mass is:
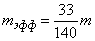
(6)
Thus, calculating
and knowing the coefficient of stiffness
defined by formula (12) in chapter 2.1.2 the eigenfrequency of the cantilever oscillation can be expressed as a function of its parameters in the following way:
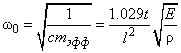
(7)
where
– cantilever density,
– Young's modulus. As can be seen from (6),
is inversely as the square of the beam length. This fact should be taken into consideration when choosing a cantilever. The cantilever eigenfrequency must be as high as possible, otherwise its natural oscillations will be readily excited due to the probe trace-retrace move during scanning or due to external vibrations influence.
Summary.
- To employ AFM techniques based on the probe vibration, one should know the cantilever eigenfrequency and effective mass.
- The effective mass is given by: .
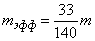- The eigenfrequency is
.