1.3.2 Current-Distance Characteristic
Measurement of relation between tunneling current and tip-sample distance is carried out in
spectroscopy mode. According to (11) from chapter 1.2.1, in absence of a condensate, a typical current-height relation is an exponential current decay (Fig. 1) with a characteristic length of a few angstrom [1, 2].
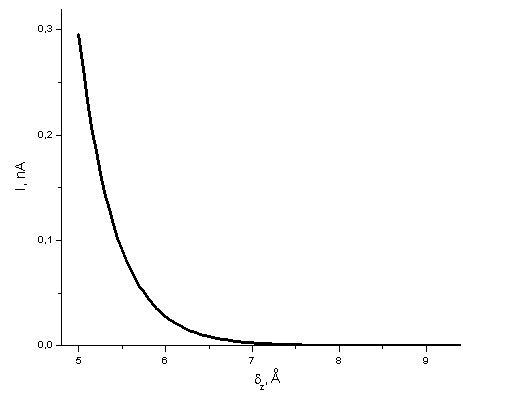
Fig. 1. Theretical
curve for Pt sample and Pt-Ro probe.
Inspecting an experimental
curve, it is possible to estimate the potential barrier height
. If tip-sample bias
is small enough, then according to chapter 1.2.2, tunneling current can be written as
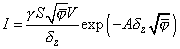
(1)
where
,
,
– contact area,
– free electron mass,
– elementary charge,
– Planck's constant.
From (1)
can be expressed through some analytical function of
. Finding the natural logarithm of (1) and differentiate the result by
one can obtain
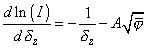
(2)
If
, then
can be expressed from (2) by following way
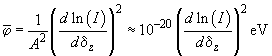
(3)
where
is experessed in m-1. Emphasize, that in most cases the condition
realizes practically always. For instance, if
, then expression (3) will be correct at
.
Experimental
curve for Pt-flim which was measured using Pt-Ro probe in STM (Solver P47) on air, is shown on Fig. 2.
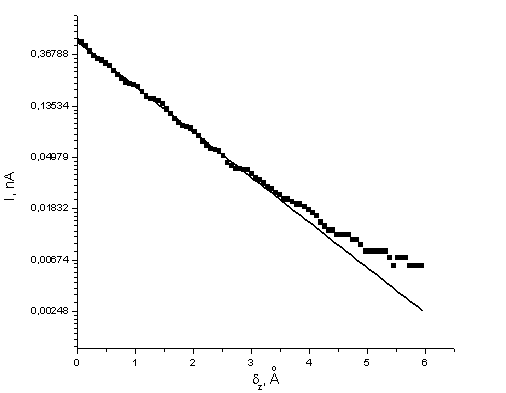
Fig. 2. Experimental
curve (semilogarithmic scale).
Solid line – approximation
.
Substituting value of approximated straight line slope
in (3), we obtain, that
. Theoretical value of
, in case, then both electrodes are produced from Pt, equals
. Thus, experimental value of
is lower by a factor about 6 than theoretical one. Most probably, the main reason of this difference is condensate presence on electrodes surface. Even for fresh surfaces of pyrolitic graphite at maximum
values, the corresponding values of
are less than several tenths of eV. These values are deliberately less than those known from high vacuum and low temperature STM experiments for the same samples and tips [3]. Values
of derived from experiments in air are close to those obtained using STM configured for electrochemical measurements in situ when liquid polar medium exists between sample and tip [3]. A condensate in the STM operating in air is evidently the analogue of such a medium. Thus, the condensate occurence on the sample surface results in the STM image quality deterioration and values of
understatement.
Frequently
spectroscopy is used for a determination of tip quality (sharpness). Experimental
curves, which are measured at investigation of HOPG surface using "good" and "poor" sharp tip of Pt-Ro probe, is shown on Fig. 3, 4.
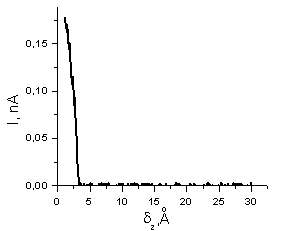
Fig. 3.
spectroscopy for a "good-shape" STM tip.
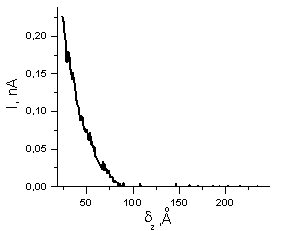
Fig. 4.
spectroscopy for a "poor-shape" STM tip.
Tip quality criterion is following: 1) if tunneling current drops twice at tip-sample distance less than 3 Å, then tip quality is very good; 2) if this distance is about 10 Å, then atomic resolution can be still obtained on HOPG using such STM tip; 3) if the current drops at distance equals or more than 20 Å, then this STM tip should be replaced or sharpened [4].
Summary.
- It is possible to estimate electron work-function of investigated material using
spectroscopy (3).
- The difference between experimental and table values of work-function is connected with the condensate presence on electrodes surface.
- In practice
curve is used for a determination of STM tip quality (sharpness).
References.
- John G. Simmons. J. Appl. Phys. – 1963. – V. 34 1793.
- G. Binnig., H. Rohrer. Helv. Phys. Acta. – 1982, – V. 55 726.
- S. Yu. Vasilev, A. V. Denisov. Journal of technical physics. – 2000, – vol. 70, num. 1 (in Russian).
- NT-MDT. Solver P47 users guide.