2.3.5 Approach-retraction curves

Consider a cantilever oscillations near a sample surface. As shown in chapter 2.2.1, the tip-sample interaction potential has a characteristic appearance depicted in Fig. 1. As the cantilever touches the sample and deforms its surface, the force of elastic repulsion prevails. At the tip-sample separation on the order of a few tens of angstrom, the intermolecular interaction called the Van der Waals force predominates.

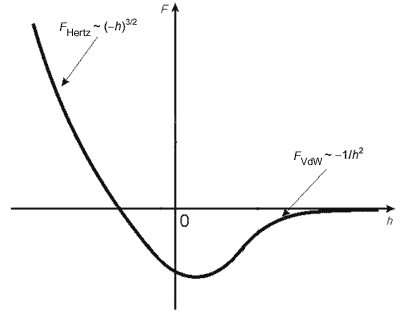
Fig. 1. Typical appearance of the tip-sample interaction potential.

As shown in chapter 2.3.4, the presence of external force dependent on spatial coordinates, gives rise to the change in resonance properties of the cantilever-sample oscillating system.

Change in the oscillations phase:

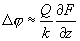(1)

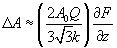change in the oscillations amplitude:

(2)

change in the resonant frequency:

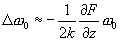(3)

where - cantilever stiffness, – oscillating system Q-factor, – cantilever oscillations amplitude in the absence of external force.

Thus, measuring dependence of the oscillations resonant frequency, phase or amplitude on the tip-sample separation, one can render the derivative appearance and, in some cases, the interaction force itself. The corresponding experimental curves are called the approach curves (Fig. 2).

Fig. 2. The tip-to-sample approach curves. – amplitude of the cantilever oscillations at resonant frequency,
– resonant frequency in the absence of the external force gradient.