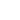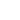2.2.7.4 The Maugis model of solids adhesion

The Maugis mechanics [1] (1992) is the most composite and accurate approach. It can be applied to any system (any materials) with both high and low adhesion. The amount of adhesion is determined by parameter :

(1)

where – interatomic distance.

DMT and JKR models are extreme cases of the Maugis mechanics corresponding to different parameters . For the stiff materials (DMT) , for compliant materials (JKR) .

Fig. 1a. Applicability of the Maugis model.

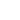
Fig. 1b. Plot of the force vs. the penetration depth.

The Maugis model assumes that the molecular attraction force acts within a ring zone at the contact area border. The Maugis correction to the Hertz problem solution is expressed implicitly via parameter :

(2)

where – tip curvature radius, – contact area radius, – effective Young's modulus , – work of adhesion (see chapter 2.2.7.1).

Both JKR model and Maugis mechanics adopt originally the existence of hysteresis during the approach-retraction cycle. It is assumed that during the cantilever approach the attraction force arises sharply at the moment of touching, then the system proceeds from point 0 into point 1 (Fig. 2). During the cantilever retraction the system "describes" the other path 1-2 until the jump out of the contact occurs 2-3.

Fig. 2. Plot of the force vs. the penetration depth for Maugis model at approach-retraction cycle.

The loop 0-1-2-3 in the plot means that to separate the probe from the sample some work must be done which is equal to the loop square. This is the work of adhesion .

References.

Maugis D.J., J. Colloid. Interface Sci. 150, 243 (1992).