2.2.2.2 The Hertz problem solution
The general solution to this problem is well known (see chapter 2.2.2.3) though it is written in an implicit form [1]. In order to get the general idea of the deformations in elastic contact and obtain characteristic numerical values, we will confine to the analysis of two spherical surfaces interaction – the tip and the small sample area. This means that
 ,
,
 .
.
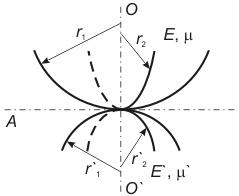
Fig. 1. Hertz problem definition.
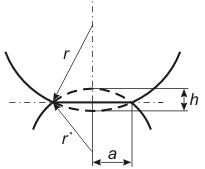
Fig. 2. Relation between contact area radius
 and penetration depth
and penetration depth
 in deformed state.
in deformed state.
Under the load the contacting bodies deform in such a way that instead of a contact point some contact area arises. Since the problem symmetry is axial, this area is clearly circular. Denote its radius by
 .
.
Let us introduce the following convenient quantities:
 and effective Young's modulus of the given pair of materials:
and effective Young's modulus of the given pair of materials:
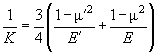
(1)
At small deformations (assumption 3 in chapter 2.2.2.1) the following geometric relation between penetration depth
 and contact circle radius
and contact circle radius
 is valid:
is valid:
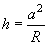
(2)
which is clear from Fig. 2.
The Hertz problem solution relates the loading force
 and the penetration depth
and the penetration depth
 :
:
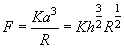
(3)
Accordingly, the pressure is the following function of the force:
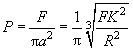
(4)
The given solution for the case of two spherical bodies contact includes one important special case of the flat sample contact with the tip having curvature radius
 (
(
 ,
,
 ).
).
Let us depict the Hertz problem solution, i.e. the dependence of the penetration depth (horizontal axis) upon the loading force (vertical axis) for positive
 . In Fig. 3, the rising branch corresponds to the Hertz problem solution.
. In Fig. 3, the rising branch corresponds to the Hertz problem solution.
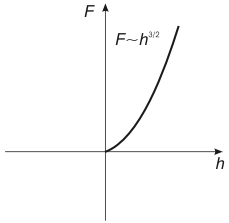
Fig. 3. Force depending on penetration depth 
(graph of the Hertz problem solution).
As mentioned above, the solution can be obtained in implicit form for any kind of surfaces (stipulated in condition 2 in chapter 2.2.2.1), however our goal is an exact numerical result. Nevertheless, this result by the order of magnitude is the same as in our simplified case. Therefore, we can estimate the characteristic contact pressure from formula (4).
Results are tabulated in tables which present magnitudes of contact area and pressure at various Young's modulus of a studied material. The data are calculated for the silicon cantilever –
 – with the curvature radius
– with the curvature radius
 at two loading force magnitudes
at two loading force magnitudes
 and
and
 .
.
| Sample Young's modulus, Pa | Contact area radius  , nm , nm |
Penetration due to deformation  , nm , nm |
Contact pressure  , GPa , GPa |
|||
| 108 | 7.2 | 16 | 5.2 | 24 | 0.03 | 0.07 |
| 109 | 3.4 | 7.2 | 1.1 | 5.2 | 0.14 | 0.3 |
| 1010 | 1.6 | 3.4 | 0.25 | 1.1 | 0.63 | 1.4 |
| 1011 | 0.9 | 1.8 | 0.07 | 0.3 | 2.2 | 4.7 |
| 1012 | 0.7 | 1.4 | 0.04 | 0.2 | 3.7 | 7.9 |
at loading force  , nN , nN |
||||||
| 5 | 50 | 5 | 50 | 5 | 50 | |
| Material and its Young's modulus | Contact area radius  , nm , nm |
Penetration due to deformation  , nm , nm |
Contact pressure  , GPa , GPa |
|||
Quartz glass, |
3.74 | 8.04 | 1.04 | 6.46 | 0.11 | 0.25 |
Kapron, |
3.24 | 6.98 | 1.05 | 4.87 | 0.15 | 0.33 |
Copper, |
0.79 | 1.7 | 0.062 | 0.29 | 2.55 | 5.51 |
Tungsten, |
0.68 | 1.46 | 0.046 | 0.21 | 3.44 | 7.47 |
Diamond, |
0.64 | 1.38 | 0.041 | 0.19 | 3.88 | 8.36 |
at loading force  , nN , nN |
||||||
| 5 | 50 | 5 | 50 | 5 | 50 | |
It is clearly seen that the contact pressure is higher for more stiff samples.
The other restriction (assumption 1 in section 2.2.2.1) is the problem solution within the model of the continuum with isotropic characteristics. Naturally, on the microlevel, the molecular structure is of great importance, therefore such assumption is rather relative. That is why the Hertz problem solution with a more exact geometrical characteristics of contacting surfaces (in contrast to the considered case) makes no sense because assumption 1 in section 2.2.2.1 itself is a very crude approximation.
Summary.
- In a place of a "point" contact of the tip and the surface the contact area is produced.
- The Hertz problem solution allows to find the contact area radius and penetration depth as a function of applied load.
- Typical magnitudes for the AFM are as follows:
- contact area radius – up to 10 nm;
- penetration depth – up to 20 nm;
- contact pressure – up to 10 GPa.
References.
- Landau L.D., Livshits E.M. Theory of elasticity. – Nauka, 1987. – 246 p. (in Russian)
- Gallyamov M.O., Yaminsky I.V. Scanning probe microscopy: basic principles, distortions analysis (218 kB).